Очень интересные слайды про A/B эксперименты от чуваков из Bing: “Seven Rules of Thumb for Web Site Experimenters”: https://exp-platform.com/Documents/2014-08-27ExperimentersRulesOfthumbKDD.pdf
Куча разных примеров. Особенно мне запомнились вот эти штуки.
- Twyman’s Law: Any figure that looks interesting or different is usually wrong.
Если статистика (или результаты эксперимента) выглядит необычно, удивляет, показывает какие-то невероятные результаты — скорее всего где-то ошибка и надо в первую очередь искать ее. Главная ошибка: сразу объяснять удивительный результат неверной причиной (например результатами эксперимента). - Пример неправильного объяснения: цинга и витамин C.
Цинга была серьезной проблемой в 16-18 веках у моряков. Доктор James Lind обратил внимание на отсутствие цинги у кораблей в Средиземном море. В 1747 году он провел эксперимент и давал одним морякам лаймы, другим обычную еду. Чуваки, кто ели лаймы не заболели. Но Lind сделал неправильный вывод и объяснил успех неверной причиной. Позже в Англии он начал лечить пациентов с цингой концентрированнным лимонным соком. К сожалению в процессе его приготовления его подогревали, что разрушало витамин C. Поэтому у доктора не получилось повторить успешный результат и он разочаровался в своей теории (и стал лечить цингу кровопусканием). - Второй пример: известная история от Гугла.
Когда они увеличили количество результатов на странице с 10 до 20, скорость загрузки страницы выросла на полсекунды, а revenue (заработок с рекламы) снизился на 20%. Это объясняли как “смотрите как скорость влияет”. Чуваки из Бинга задумались — да, скорость влияет, но неужели 500ms влияет на 20% (!) revenue со страницы. Стали копать и повторили эксперимент. По их словам дело не в скорости, а в кол-ве рекламы на странице. На странице с 10 результатами — определенное количество рекламных объявлений. Когда количество результатов увеличивается, а количество объявлений остается тем же — это понижает их видимость (ну и соответственно клики и заработок). Они увеличили количество рекламы (еще больше замедлив страницу) и влияние на revenue исчезло. - Часто эксперименты не улучшают engagment или abandonment rate, а всего лишь направляют клики/путь пользователя в другое место. Поэтому важно смотреть, не каннибаллизируют изменения просто существующий трафик, не улучшая картину в целом. Надо смотреть на улучшение общей метрики и если уж каннибализировать существующие клики, то направлять их на области, которые чем-то лучше чем существующие. Перефразируя: легко оптимизировать локальные штуки (использование фичи, кликабельность элемента и тд) — сложно улучшать глобальные штуки (общие метрики, общий успех).
Хорошее видео про поиск и найм продакт-менеджеров: “Find, Vet and Close the Best Product Managers”:
Текстовая версия: https://firstround.com/review/find-vet-and-close-the-best-product-managers-heres-how/
Две штуки интересны даже тем, кто не нанимает себе продактов в команду.

Must have и should have скиллы у продактов. Автор говорит, что 1) must have силлы обязательны 2) хороший продакт имеет все из must have и половину из should have 3) крутой продакт имеет все и из must have и should have
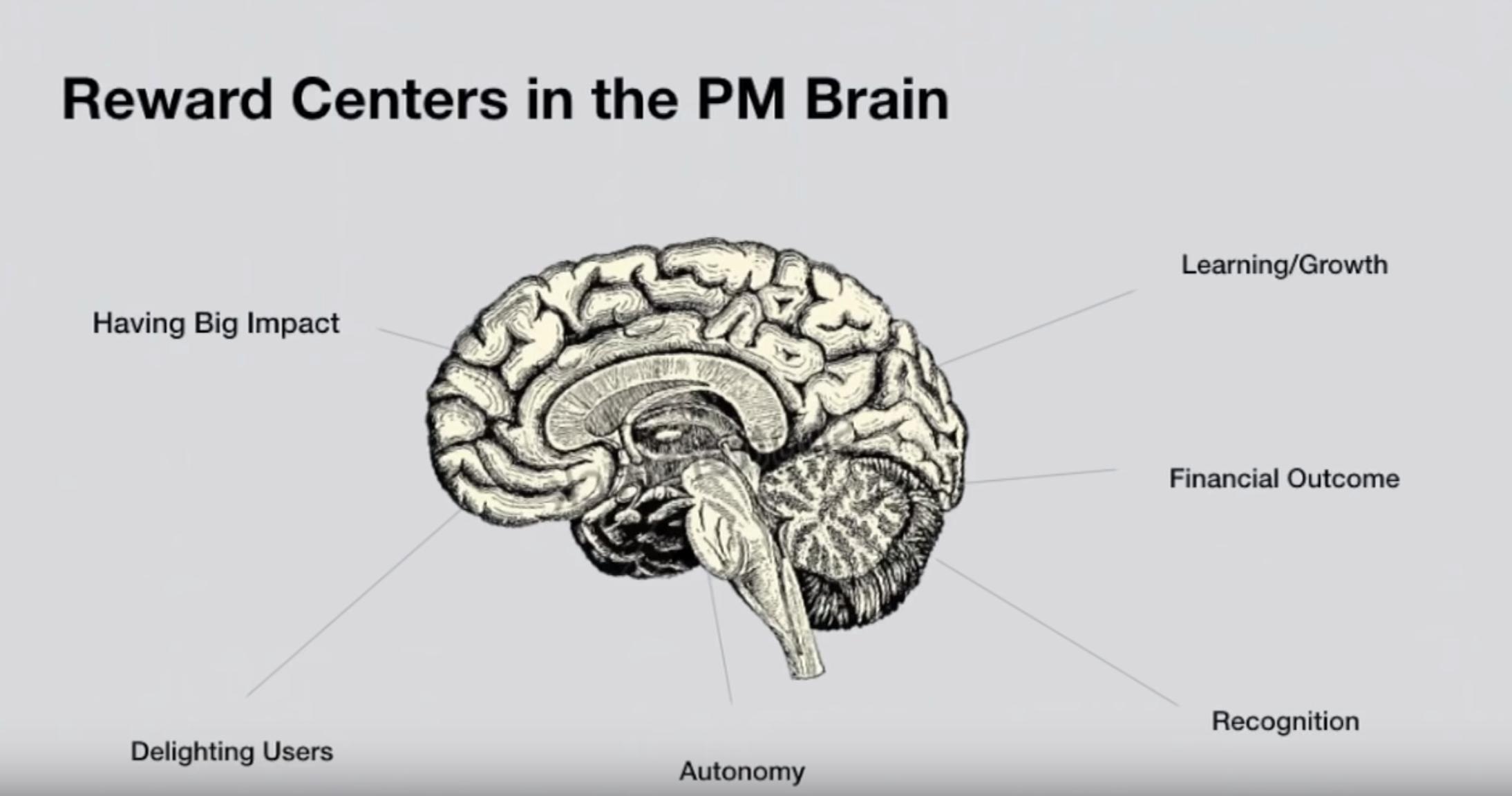
Что мотивирует продакта. Самое важное причем это impact, delighting users и autonomy.
Если спросить продакта про data-driven (ок-ок, data-informed) подход, то конечно он скажет, что это правильно и надо все считать. На практике же перейти от подхода “делаем, что сердечко попросит” к “смотрим на числа, а потом делаем” сложно (и не всегда нужно).
Резкий переход от “выбора сердцем” к выбору фич только через расчеты или сломает работающие текущие процессы или же родит бюрократические кафкианские таблицы с кучей полей и баллов. А на деле по прежнему выбор будет делаться как и раньше (если продакт хочет фичу — он без задней мысли нарисует там столько баллов, что таблица скажет делать эту фичу первой), только теперь надо кучу таблиц заполнять.
Переход должен быть осмысленный. Поэтому если сейчас вы совсем не смотрите на данные при выборе фич, но хотите начать — может подойти вот такой вот путь.
- Шаг 1: считаем данные после выпуска. Ничего не меняем в выборе фич. Выбираем как и раньше. Но после того, как каждое новое изменение выпущено, cчитаем его метрики использования: как часто использовали эту фичу, как именно (базовые штуки).
Этот первый шаг уже заставить сделать две вещи: начать считать хоть что-то (то есть построить базовую инфраструктуру аналитики) и смотреть на реальное использование фичи в жизни (сюрпризы вида “я думал будет популярная штука, а использовало три человека” бодрят).
- Шаг 2: делаем предсказания перед началом разработки и считаем данные после выпуска. Ничего не меняем в выборе фич. Выбираем как и раньше. Но теперь после выбора фичи делаем предсказание про ее использование, например “как много народу ее будет использовать?”. Предсказание записываем. После выпуска собираем аналитику (мы это научились уже делать в шаге 1) и сравниваем.
Этот шаг заставляет нас научится делать базовую оценку ДО выпуска фичи и сравнивать потом предсказание с реальным результатом, давая обратную связь. Это учит делать лучшие предсказания и учит, что наши предсказания часто ошибочны.
- Шаг 3: делаем предсказания перед началом разработки, они влияют на выбор. У нас уже есть backlog изменений. Делаем предсказания (по сути строим модель или прикидываем будущее использование) про каждое изменение. Предсказания с максимальным результатом имеют сильное влияние на наш выбор, что делать.
На этом шаге мы уже используем оценку для лучшего выбора. В следующий шагах уже можно делать более сложные оценки (например уже считать влияние на деньги и учитывать затраты на разработку).
Важное замечание: я (пока) противник использования подхода, когда для выбора “что делать” используются только расчеты: ввел в кучу колонок данные и оно сказало, что делать. На мой взгляд такой подход не дает выйти из локального максимума, заставляет игнорировать области, влияние которых сложновычислимо (дизайн и скорость, например), не учитывают стратегические вещи и так или иначе не убирают субъективный выбор человека (баллы же он там сам проставляет). Поэтому я за подход “данные помогают принять решение что делать”, когда они влияют на выбор и помогают избавится от ошибок решений, но не задают выбор сами.
Slava Akhmechet (был продактом в Stripe, построил RethinkDB) пишет в Твиттере (с тех пор он удалил эти два своих твита) описания стратегий, которые помогают решать сложные проблемы. За несколько лет наблюдений за кучей проблем и кейсов он обнаружил, что их решения сводятся к ~20 стратегиям. Пока он запостил две.
1. Radical quantification.
TL;DR: transform an arbitrarily complex problem into a trivial one by picking just one quantifiable dimension to worry about.
Свести проблему к одному главному числу и думать только о нем.
Here is a trivial example: Net Promoter Score. You take an extremely complex problem of product/service satisfaction and distill it to one number – “would you recommend this to others?”
…
Consider a problem: how much did real wages grow from 1800-1992? The problem is extremely complex because it requires properly computing inflation in presence of rapid technological change and incomplete economic data. Is there a way to solve it with radical quantification? Here is a solution by William Nordhaus (Nobel Prize in economics in 2018). Reduce the problem to a single dimension – how many hours did the average person have to work to produce a lumen of light? This isn’t easy to compute, but it makes an impossible problem tractable.
…
You can project nearly every dimension into another one - money. That lets you compare seemingly incomparable things.
…
One of the coolest things about radical quantification is that you don’t even have to pick a dimension you can observe because the technique is extremely susceptible to using proxy metrics. You just have to be really creative about picking the unit.
2. Near/far transformation.
TL;DR: our brain has two sets of heuristics to quickly parse complex streams of information. Manually tricking it to shift into a different mode can make seemingly intractable problems trivial.
Переключать себя между двумя режимами: ближний (личное, детали, эмоции, внимание) и дальний (асбтрактное, объективное, взгляд сверху, отстранненность).
A way to make a difficult problem simple is to reframe a far mode problem in near mode. Simple example. Far mode: how do I pick a VC? Near mode: can I stand working with Bill for ten years? You’ve outsourced a hard problem to your gut for an immediate answer!
…
Another similar trick: convert a continuous space into discrete units. Paul Graham did this in his Life is Short essay. How many Christmases do you have with your children? Waitbutwhy did it with Your Life in Weeks calendar.
…
Another example of far->near mode. Here are WhatsApp founders describing the very complex question of online advertising: “no one wakes up excited to see more advertising; no one goes to sleep thinking about the ads they’ll see tomorrow”.
…
We tend to think of ourselves in near mode (great detail) and of others in far mode (abstractly). Flipping the two can make us seem dramatically more attentive. And when you hear internet advice that “nobody thinks about you that much”, what it really means is that when they do think about you, they think about you in far mode. Of course there is the opposite trick too – trick yourself to shift from near mode to far mode to get some objectivity.
…
Describing current events in far mode can make one seem more profound by giving people some objectivity. Shifting your mind into far mode can help you make objective political decisions (especially if you’re highly attached to your current reality, which we usually are). “So if you’re considering the worthiness of a particular statue […] Pretend you’re from some very distant foreign country and view the dispute through that more objective lens.”
…
A far mode trick that can help make decisions – imagine multiple futures and pick between them. […] And a near mode version of this – imagine you’re already in a counterfactual future, and decide whether you’d want to come back.
Десять тысяч A/B тестов
Большой текст. Будет интересен тем, кто знает, что такое A/B тесты и статистическая значимость.
A/B тесты полезная штука для валидации гипотез, но не такая простая как кажется — легко ошибиться. Если о статистической значимости и p-значениях большинство знает, то вот о более хитрых возможностях ошибиться — нет.
Одна из проблем: repeated significance testing error (повторные ошибки тестирования значимости). Умные люди пишут (русский перевод), что выборка должна быть фиксированной, например “в тесте поучаствует 1000 посетителей”. После чего тест нужно обязательно завершить и подсчитать результаты.
Нельзя завершать тест досрочно, если он вдруг показал статистическую значимость раньше. Нельзя держать тест запущенным так долго, пока какой-то вариант не покажет статистическую значимость(без ограничения на размер выборки).
Эта мысль контринтуитивна для меня. Я знаю, что про это пишут люди, которые понимают в статистике больше чем я (я понимаю так себе). Но я не мог понять до конца и осознать по настоящему почему оно работает так. Мысли об этом меня преследовали и воскресной ночью я понял — надо сделать модель и просимулировать всё это!
Я сделал модель, которая симулирует множество A/B тестов, сравнивая две гипотезы с разной конверсией. В каждой симуляции трафик случайным образом распределяется между двумя версиями. Каждый симулированный посетитель случайным образом конверится, согласно конверсии у гипотезы. Мы собираем статистику и оцениваем:
- ситуации с досрочным завершением теста, если появилась статистическая значимость;
- ситуации завершением с ограничением по выборке
- и ситуации когда тест идет бесконечно долго, пока не появится статистическая значимость в одном из вариантов.
Сам код можно найти на Гитхабе. Также я там подробнее описал подход к симуляции. Если вы увидели ошибку в коде или же расчетах — пожалуйста, расскажите мне (@qetzal в Телеграме) — я буду очень благодарен (я не настоящий программист и статистик.
Ниже я расскажу про результаты (много чисел). Я просимулировал три ситуации:
- две гипотезы сильно отличаются по конверсии,
- отличаются немного
- и не отличаются совсем
В каждой ситуации мы смотрим и на результат после фиксированной выборки (26000 посетитилей, то рекомендованное число для 3% baseline конверсии, обнаружения разницы в 20% и 95% стат. значимости). Каждая ситуация была просимулирована 10,000 раз — проценты ниже отображают ситуации от всех симуляций.
Ситуация первая — гипотезы сильно отличаются по конверсии
У контрольной версии конверсия 3%. У тестовой - 2.15%.
- В 99.6% случаев после фиксированной выборки мы получили правильный и статистически значимый результат.
- В 0.03% случаев после фиксированной выборки мы получили не статистически значимый результат.
- В 87% случаев статистическая значимость наступила раньше чем прошла вся фиксированная выборка. Результат был правильным (мы определили, что тестовая версия хуже конвертит). То есть тут мы могли завершить тест раньше чем прошла вся фиксированная выборка и были бы правы.
- В 13% случаев статистическая значимость наступила раньше чем прошла вся фиксированная выборка. Но результат был неправильным, мы бы ошибочно посчитали, что контрольная версия конвертит хуже, хотя это не так (это тестовая заметно конветит хуже).
Вывод: Фиксированная выборка показала значимый и правильный результат в 99.6% случаев (ожидаемо).
Если мы завершаем тест раньше, как только получили значимость и версии сильно отличаются по конверсии, то в ~87% случаев можно это сделать и получить верный результат. Это может сэкономить время. Но в 13% случаев такой подход приводит к ошибке и неправильному выбору — даже при такой большой разнице в конверсиях.
Ситуация вторая — гипотезы отличаются по конверсии, но не сильно
У контрольной версии конверсия 3%. У тестовой - 2.8%.
- В 75.2% случаев после фиксированной выборки мы получили не статистически значимый результат (то есть мы не смогли достоверно определить какая гипотеза конвертит лучше). Это ожидаемый результат, так как разница в конверсии гипотез меньше, чем 20%, заложенная в расчете рекомендованной выборки (26000 посетителей).
- В 24.4% случаев после фиксированной выборки мы получили статистически значимый и правильный результат.
- В 0.4% случаев после фиксированной выборки мы получили статистически значимый и неправильный результат (редкое событие)
- В 54.8% случаев статистическая значимость наступила раньше чем прошла вся фиксированная выборка. Результат был правильным (мы определили, что тестовая версия хуже конвертит). То есть тут мы могли завершить тест раньше чем прошла вся фиксированная выборка и были бы правы.
- В 15.8% случаев статистическая значимость наступила позже чем прошла вся фиксированная выборка. Результат был правильным (мы определили, что тестовая версия хуже конвертит). То есть тут мы могли подержать тест чуть подольше и получить конкретный результат несмотря на то, что фиксированная выборка ничего не показала.
- В 29.1% случаев статистическая значимость наступила раньше чем прошла вся фиксированная выборка. Но результат был неправильным, мы бы ошибочно посчитали, что контрольная версия конвертит хуже, хотя это не так (это ведь тестовая конвертит хуже).
Вывод: если версии не сильно отличаются по конверсии (но отличаются), то при недостаточно большой фиксированной выборке мы будем получать не статистически значимые результаты (в нашем случае 75% случаев). Значимые и правильные результаты были получены только в четверти случаев по результатам фиксированной выборки. Это ожидаемый результат — если нет уверенности в сильной разнице гипотез надо делать выборку больше.
Если мы завершаем тест раньше, как только получили значимость, и версии не сильно отличаются по конверсии, то в ~54% случаев можно это сделать и получить верный результат. В 15% можно подержать тест запущенным уже после того как прошла фиксированная выборка (которая не показала значимость) и все таки получить значимый и правильный результат.
Но вот уже в 29% случаев (каждый третий!) такой подход приводит к ошибке и неправильному выбору. Мы останавливаем тест раньше и получаем значимые результаты, что контрольная версия конвертит хуже (что не так).
Ситуация третья — гипотезы не отличаются по конверсии
У контрольной версии конверсия 3%. И у тестовой — 3%. (спойлер — тут начинается самое веселое)
- В 90% случаев после фиксированной выборки мы получили не статистически значимый результат (то есть “мы не смогли достоверно определить какая гипотеза конвертит лучше”). Это ожидаемый результат, так как разница в конверсии гипотез нет.
- В 5% случаев после фиксированной выборки мы получили статистически значимый и правильный результат.
- В 5% случаев после фиксированной выборки мы получили статистически значимый и неправильный результат (ожидаемо)
- В 78.6% случаев (!) статистическая значимость наступила раньше чем прошла вся фиксированная выборка. И результат был неправильным — мы подумали, что у какой-то версии преимущество (а они одинаковые).
- В 12.9% случаев статистическая значимость наступила позже чем прошла вся фиксированная выборка. И результат был неправильным — мы опять подумали, что у какой-то версии преимущество.
- В 8.5% случаев статистическая значимость так и не наступила, как долго мы тест не держали запущенным (в симуляции тест автоматически завершался, если было больше миллиона посетителей)
Вывод: если версии не отличаются по конверсии и мы завершаем тест после фиксированной выборки, мы будем получать не статистически значимые результаты в большинстве случаев (в нашем случае 90% случаев). В 5% случаев мы получим значимые и неправильные результаты — процент таких ошибок ограничен сверху нашим “p-value”, мы можем его снижать (увеличивая выборку), но он не будет больше.
Если отличий в гипотезах нет и мы или завершаем тест раньше (до окончания фиксированной выборки) как только получили первый значимый результат или держим тест запущенным пока не получим значимый результат — мы получим значимые и неверные данные (что какая-то гипотеза отличается) в 91.5% случаев. 9 из 10 неверных ответов. Wow.
Выводы
-
Эти симуляции показывают, что если мы запускаем эксперимент не на выборке с заранее определенным размером, а просто останавливаем его как только получили значимые результаты, то мы будем получать ошибки. Если гипотезы сильно отличаются — в 10% случаев мы выберем худшее решение. Если не сильно, то в 29% случаев (каждый третий!). Если гипотезы не отличаются — в 91.5% случаев, в девяти из десяти экспериментов мы убедим себя (“там же статистическая значимость!”) в том, чего нет и будем это делать в полной уверенности, что это приносит пользу (а не приносит)
-
Компании и консультанты, которые показывают выигрыш теста как только появился значимый результат (до теста на всей фиксированной выборке, если используется стандартный подход к вычислению стат. значимости) — хитрят и обманывают. Они показывают много false positives, якобы успехов тестов. Особенно у начинающих, которые тестируют практически одинаковые гипотезы типа “зеленая кнопка против красной”. Таким образом они создают фальшивое ощущения прогресса “ого, A/B тесты как круто работают — я тут заимплементил кучу гипотез и ща у меня все в гору пойдет”.
TL;DR: Надо заранее выбирать размер выборки, останавливать тест когда он прошел и измерять значимость только в конце. Если тест не значимый — надо его перезапускать (а не продолжать). Если тест не значимый — возможно эффект изменений слишком мал для детектирования, надо увеличивать выборку.
P.S. Читатель Igor Yashkov прислал (спасибо большое!) еще интересных ссылок, которые открывают еще одну интересную штуку.
С одной стороны уже понятно, что останавливать тест раньше или держать его дольше, чтобы достичь стат. значимости — нехорошо, так как легко принять неправильное решение.
С другой стороны — это очевидно неудобно. Каждый тест надо держать запущенным до заранее определенного конца (при не таком частом событии, например апгрейд до платного плана и небольшой разнице в гипотезах это может занять недели и месяцы). Тест может не показать статистическую значимость и значит надо все или начинать заново (еще месяц!) или выкидывать сделанную работу.
Люди пытаются обойти эту проблему, используя другие подходы к расчетам, без p-value (то что все используют c p-value называют frequentist hypothesis testing).
Один из подходов это Bayesian A/B Testing. Очень подробно про него пишет VWO. При каждом свидетельстве (есть конверсии или нет) мы обновляем вероятности гипотезы. При таком подходе мы можем и остановить тест в любой момент и держать его запущенным так долго как хотим. VWO говорит, что это заметно ускоряет тесты. Это сильно уменьшает процент ошибок, но говорят не убирает их совсем.
Или вот еще один другой подход: frequentist approaches to sequential testing.
Но конечно никто как правило эти хитрые другие подходы не использует. У всех стандартный подход, который уязвим к ошибкам в случае ранних остановок.
(в ссылках выше много математики — я сходу не понял все штуки, потребуется сесть и обдумать)
Intercom апселлит новые фичи на экране добавления нового пользователя в систему. Интересный подход.
У Теодора Рузвельта есть сильная цитата:
Не критик имеет значение, не человек, указывающий, где сильный споткнулся, или где тот, кто делает дело, мог бы справиться с ним лучше. Уважения достоин тот, кто сам стоит на арене, у кого лицо покрыто потом, кровью и грязью; кто отважно борется; кто совершает промахи и ошибки, потому что никакой труд не обходится без них; кто познал великий энтузиазм и великую преданность, кто посвящает себя достойной цели; кто, при лучшем исходе, достигает высочайшего триумфа, а при худшем, если его постигает неудача, это по крайней мере неудача в великом дерзновении; и потому никогда он не будет среди тех холодных и робких душ, которым не знакомы ни победа, ни поражение.
Эта мысль повторяется и у Нассима Талеба, который вводит понятие “skin in the game” (“шкура на кону” в русском переводе). Главная идея у него: мнение/убеждение не надо принимать во внимание, если высказывающий это мнение/убеждение не несет рисков из-за возможной ошибочности этого мнения. Ассиметрия рисков от мнения/решения — плохо.
Очевидно (для меня), что полное игнорирование мнения окружающих — неэффективный подход. Даже мимо проходящий человек или вечный критик может дать ценный полезный фидбэк. Когда владелец ресторана игнорирует жалобы посетителей со словами “откройте свой ресторан и потом жалуйтесь” это выстрел себе же в коленку.
Но это хороший подход к тому, какой вес стоит давать фидбэку, отзыву или совету. Если человек сам “на арене” и ставит что-то на кон (не важно в той же области или нет), то его слова значат больше, чем у остальных. Если же человек “не на арене”, избегает рисков от своего мнения/решения/выбора — окей, его фидбэк тоже надо рассмотреть, но с меньшим весом.
Большая открытость к фидбэку несет в себе парадокс (я уже писал про это недавно) — мнение есть у всех, мнения противоречат друг другу и твоим целям. Легко зависнуть в выборе или принимать во внимание людей, которые не разбираются в том, о чем говорят. Штука выше помогает этот парадокс решить.